11.19. High-level interface: Optimal EV charging and speed profile example (MATLAB & PYTHON)¶
Note
We can find an updated and more realistic version of this example in Section 11.20. This example is kept in the documentation for legacy purposes.
In this example we illustrate the simplicity of the high-level user interface on an optimal electric vehicle (EV) speed and charging management. The controller plans the car’s speed and charging trajectory such that the given route is traversed in the shortest time possible, while simultaneously respecting speed limits as well as vehicle’s and battery’s technical requirements.
11.19.1. Problem Overview¶
We consider a single EV and a fixed route with given road slopes (i.e. angles) and speed limits. Optionally, some charging stations could be available at predefined locations along the road. Vehicle operation is defined by longitudinal vehicle dynamics, powertrain efficiency and battery capacity. Due to the spatial characteristic of the problem, the formulation is discretized in space domain. This problem is primarily based on the work in [JiaJibItoGor19] and [JiaJibGor20].
11.19.1.1. Vehicle Dynamics¶
Assuming a sample distance \(L_\mathrm{s}\), the longitudinal velocity of the vehicle in space domain at the discrete step \((i+1)\in\mathcal{I}\) can be determined using the velocity at the previous step \((i)\) and the difference in kinetic energy between these two consecutive steps, as follows:
where the resistance force is comprised of the following three components:
The equivalent mass \(m_\mathrm{eq}=m_\mathrm{v}(1 + e_\mathrm{I})\) includes vehicle mass \(m_\mathrm{v}\) and the effect of all rotational masses captured by the mass factor \(e_\mathrm{I}\). The road slope is represented by the road angle \(\alpha\). Variables \(F_\mathrm{t}\geq0\) and \(F_\mathrm{b}\geq0\) represent the traction and braking forces on the wheels, which are generated by the powertrain and mechanical braking system separately (note: regenerative braking capabilities could be included by allowing the traction power to be negative). The total driving resistance \(F_\mathrm{r}\) comprises rolling resistance force, gravitational force and air drag force (while neglecting the direct impact of wind speed), with \(c_\mathrm{a}\) being the air drag coefficient, \(A_\mathrm{f}\) the projected frontal area, \(\rho_\mathrm{a}\) the air density, \(g\) the gravitational acceleration, and \(c_\mathrm{r}\) the rolling resistance coefficient.
The vehicle’s velocity dynamics are thus defined by
with the assumption that the speed is constant while traversing a single discrete road segment. Note that the expression below the square root must be strictly positive in order for the problem to be feasible, as will be discussed later on. In addition to velocity, the time is also a state variable of the model and can be computed as
11.19.1.2. Vehicle Energetics¶
EV’s powertrain efficiency \(\eta(v,F_\mathrm{t},\zeta)\) is a function of vehicle’s speed, traction force and battery’s state-of-charge (SoC), as shown by the efficiency maps depicted in Figure 11.62. Nevertheless, the impact of SoC on powertrain efficiency is negligible as SoC does not change dramatically within a short time period if the battery capacity is sufficiently large. Therefore, one could generate several 2D maps of the form \(\eta(v,F_\mathrm{t})\), pre-calculated at different SoC levels such that the most accurate one can be selected according to the current SoC.
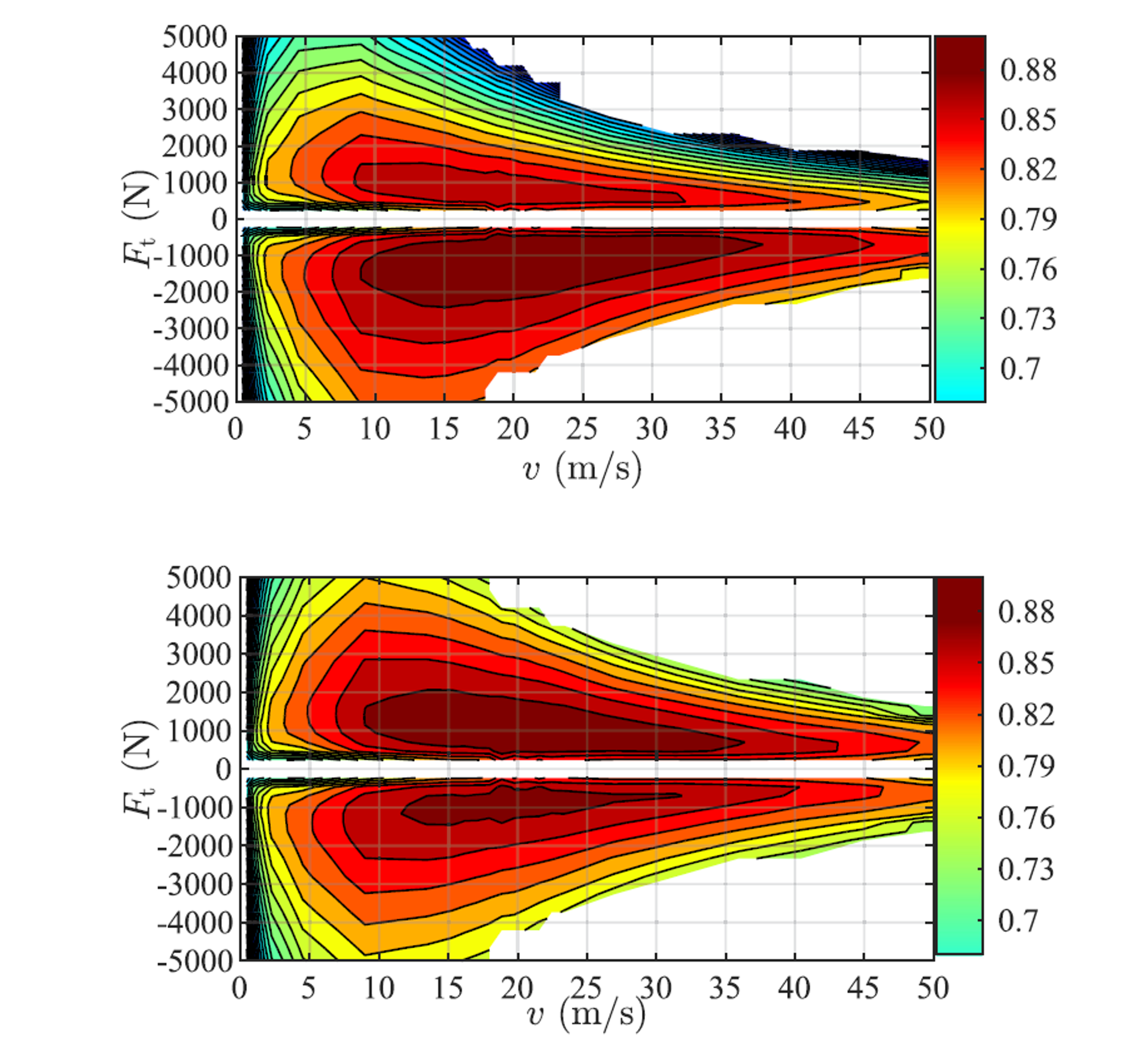
Figure 11.62 2D efficiency maps of the EV’s powertrain with two different SoC levels taken from [JiaJibGor20]: (top) \(\eta\) with SoC \(\zeta=10\,\%\); (bottom) \(\eta\) with SoC \(\zeta=90\,\%\).¶
For the purpose of this example, we have have generated a single 2D efficiency map depicted in Figure 11.63 used across all SoC levels. However, for simplicity, the implementation in this example is confined to 1D efficiency map \(\eta(F_\mathrm{t})\) extracted for \(v=15\,\mathrm{m/s}\).

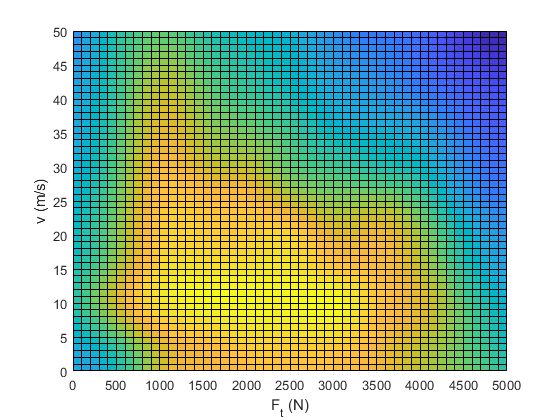
Figure 11.63 Generated 2D EV efficiency map. Note that we are using a simplified 1D efficiency map \(\eta(F_\mathrm{t})\) taken for \(v=15\,\mathrm{m/s}\) in this example.¶
The 1D efficiency map \(\eta(F_\mathrm{t})\) can be computed in the form of a cubic spline function as follows:
function [ etaMotorSpline ] = setupMotorEfficiency(FtMax)
% Returns cubic spline representing motor efficiency as a function of
% traction force.
%
% The data is taken from "Jia, Y.; Jibrin, R.; Goerges, D.: Energy-Optimal
% Adaptive Cruise Control for Electric Vehicles Based on Linear and
% Nonlinear Model Predictive Control. In: IEEE Transactions on Vehicular
% Technology, vol. 69, no. 12, pp. 14173-14187, Dec. 2020."
FtSample = 0:0.1*FtMax:FtMax;
etaSample = [0.835, 0.865, 0.9, 0.85, 0.79, 0.75, 0.72, 0.72, 0.72, 0.72, 0.72];
etaMotorSpline = ForcesInterpolationFit(FtSample,etaSample);
end
def setupMotorEfficiency(self):
"""
Returns cubic spline representing motor efficiency as a function of traction force.
The data is taken from "Jia, Y.; Jibrin, R.; Goerges, D.: Energy-Optimal Adaptive Cruise Control for Electric Vehicles Based on Linear and Nonlinear Model Predictive Control. In: IEEE Transactions on Vehicular Technology, vol. 69, no. 12, pp. 14173-14187, Dec. 2020."
"""
FtSample = np.linspace(0, self.FtMax, 11)
etaSample = np.array([0.835, 0.865, 0.9, 0.85, 0.79, 0.75, 0.72, 0.72, 0.72, 0.72, 0.72])
etaMotorSpline = forcespro.modelling.InterpolationFit(FtSample, etaSample)
return etaMotorSpline
Assuming a set of predefined charging stops at discrete spatial steps \(k\in\mathcal{K}\subset\mathcal{I}\), we can include either optional or mandatory charging at each of those stops (to be defined by the user). Given the implemented powertrain efficiency \(\eta_i(F_{\mathrm{t},i})\) and potential charging decisions, the driving energy depletion and charging instances are incorporated into the SoC dynamics at discrete step \(i\) as:
where \(E_\mathrm{cap}\) denotes the battery’s energy capacity, \(P_{\mathrm{ch},i}(\zeta_i)\) is a vehicle’s charging power dependent on the SoC, and \(\Delta t_i\) is a total charging time spent at location \(i\in\mathcal{K}\). Note that SoC \(\zeta\) is normalized on an interval \([0,1]\).
In this example we will particularly focus on the performance of a BMW i3. The charging profiles \(P_\mathrm{ch}(\zeta)\) for three production models with different battery capacities are depicted in Figure 11.64 [Fastned], and can be approximated by a piecewise-affine function shown in Figure 11.65.
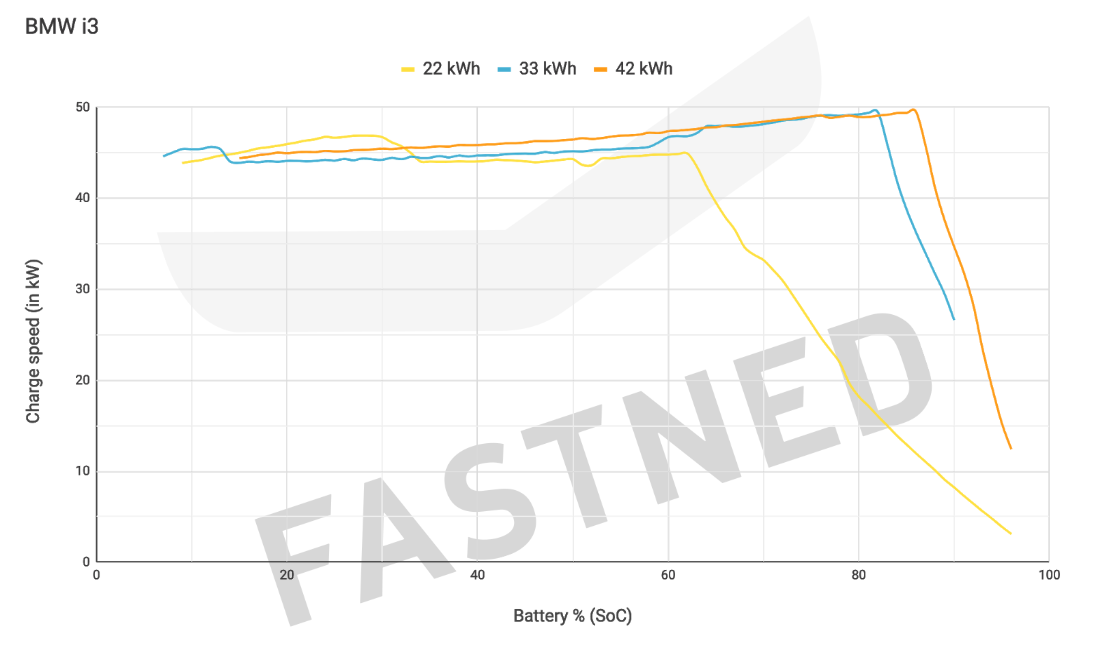
Figure 11.64 Actual charging profile of BMW i3 as a function of vehicle’s SoC.¶
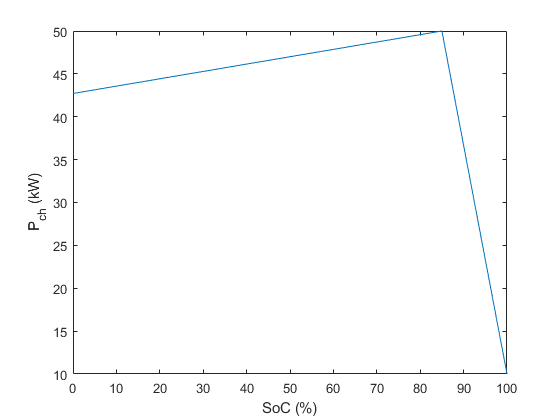
Figure 11.65 Implemented piecewise-affine charging profile for the \(42\,\mathrm{kWh}\) vehicle as a function of vehicle’s SoC.¶
The code for computing the \(P_\mathrm{ch}(\zeta)\) spline function is given below. Note that the Python implementation uses a shape-preserving piecewise-cubic representation instead of piecewise-linear one.
function [ Pch ] = setupChargingPower(PchMax)
% Returns piecewise linear representation of charging power as a
% function of vehicle's SoC.
%
% The data is taken from Fastned charging chart available at
% https://support.fastned.nl/hc/en-gb/articles/204784718-Charging-with-a-BMW-i3
%
% NOTE: Python example uses shape-preserving piecewise cubic spline
% approximation ('pchip') which might lead to negligible result
% discrepancies between the two clients when directly compared.
socSample = [0.15, 0.85, 1.0];
PchSample = [0.88, 1, 0.2]*PchMax;
Pch = ForcesInterpolationFit(socSample,PchSample,'linear');
end
def setupChargingPower(self):
"""
Returns shape-preserving piecewise cubic spline representation of charging power as a function of SoC.
The data is taken from Fastned charging chart available at https://support.fastned.nl/hc/en-gb/articles/204784718-Charging-with-a-BMW-i3
NOTE: MATLAB example uses piecewise linear approximation which might lead to negligible result discrepancies between the two clients when directly compared.
"""
socSample = np.array([0.15, 0.85, 1.0])
PchSample = np.array([0.88, 1, 0.2]) * self.PchMax
PchSpline = forcespro.modelling.InterpolationFit(socSample, PchSample, 'pchip')
return PchSpline
Clearly, the time dynamics would have to be modified as well:
with \(\Delta t_i\approx 0\) for all non-charging spatial steps \(i\notin\mathcal{K}\), and \(v_i\approx \underline{v}\) for all charging spatial steps \(i\in\mathcal{K}\), with \(\underline{v}>0\) being th lower speed bound. The latter is not set to zero for two reasons: 1) it would lead to infeasibility due to \(v_i\) being in the denominator; 2) it reflects the average speed across the distance \(L_s\), which includes both the driving and the charging instances, and is therefore greater than zero. This implies that the final vehicle model comprises three states \(x=[v,t,\zeta]^\top\) and three control inputs \(u=[F_\mathrm{t},F_\mathrm{b},\Delta t]^\top\), with the model dynamics described by
Additionally, we will include a slack variable \(s\geq0\) into control vector \(u\), as it is used to relax the upper and lower bounds on vehicle’s SoC.
11.19.1.3. Bounds¶
In terms of bounds on state variables, we impose upper and lower limits on vehicle’s velocity and SoC, dictated by the road speed limits and battery specifications:
The upper speed bound \(\bar{v}_i\) is stage-dependent, dictated by the spatial discretization of the road speed limits, whereas the lower speed bound \(\underline{v}\) is kept constant across all stages. For charging instances \(i\in\mathcal{K}\), the upper speed bound can optionally be set to \(\bar{v}_i\approx\underline{v}\), indicating that the vehicle has to reduce speed. The SoC limits \(\underline{\zeta}\) and \(\bar{\zeta}\) are also stage independent and implemented as soft bounds.
All control variables are nonnegative and upper bounded with appropriate physical and technical limits:
Here, \(\overline{\Delta t}_i\) denotes maximum permissible charging time and is set to \(\overline{\Delta t}_i\approx 0, \forall i\notin\mathcal{K}\), whereas \(\overline{F}_{\mathrm{t},i}\) and \(\overline{F}_\mathrm{b}\) are vehicle’s physical upper bounds on maximum traction and breaking force, respectively. Note that the traction force limit is comprised of the constant friction limit \(\overline{F}_{\mathrm{t}}\) and the hyperbolic traction function of vehicle’s velocity \(\overline{F}_{\mathrm{t},i}^\mathrm{hyp}(v_i)\), i.e.
as depicted in Figure 11.66. The actual function implemented in this example is showcased in Figure 11.67.
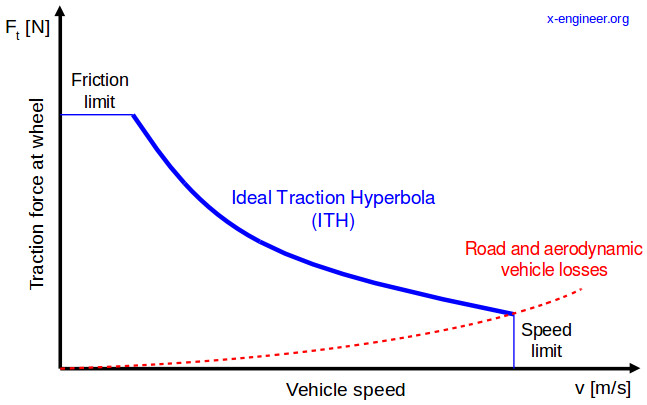
Figure 11.66 Maximum permissible traction force as a function of vehicle’s velocity taken from [xEngineer].¶

Figure 11.67 Implemented traction force hyperbola as a function of vehicle’s velocity.¶
The computation of ideal traction hyperbola \(\overline{F}_\mathrm{t,hyp}(v)\) in the cubic spline form is provided below.
function [ FtMaxHypSpline ] = setupTractionForceHyperbola(vMax,FtMax)
% Returns cubic spline representing maximum traction force as a function of
% vehicle's speed
%
% The data is generated based on the technical article provided at
% https://x-engineer.org/need-gears/
vSample = [0.25, 0.4, 0.6, 0.8, 1.0]*vMax;
FtMaxHypSample = [1.0, 0.67, 0.43, 0.32, 0.28]*FtMax;
FtMaxHypSpline = ForcesInterpolationFit(vSample,FtMaxHypSample);
end
def setupTractionForceHyperbola(self):
"""
Returns cubic spline representing motor efficiency as a function of traction force.
The data is generated based on the technical article provided at https://x-engineer.org/need-gears/
"""
vSample = np.array([0.25, 0.4, 0.6, 0.8, 1.0]) * self.kmh2ms(self.vMax)
FtMaxHypSample = np.array([1.0, 0.67, 0.43, 0.32, 0.28]) * self.FtMax
FtMaxHypSpline = forcespro.modelling.InterpolationFit(vSample, FtMaxHypSample)
return FtMaxHypSpline
11.19.1.4. MPC Formulation¶
A complete MPC problem formulation can thus be described as follows:
with the objective function explained in detail in the subsequent sections.
11.19.1.5. Model Parameters¶
As stated previously, in this example we focus on a highest energy capacity model of BMW i3, defined by the following parameters obtained from [BMWi3]:
function [ params ] = defineVehicleParameters(trip)
% Returns vehicle parameters
% Constant vehicle parameters (not to be changed)
% The data is obtained from "Technical specifications of the BMW i3
% (120 Ah)" valid from 11/2018 and available at
% https://www.press.bmwgroup.com/global/article/detail/T0285608EN/
% Gravitational acceleration (m/s^2)
params.g = 9.81;
% Vehicle mass (kg)
params.mv = 1345;
% Mass factor (-)
params.eI = 1.06;
% Equivalent mass (kg)
params.meq = (1+params.eI)*params.mv;
% Projected frontal area (m^2)
params.Af = 2.38;
% Air density (kg/m^3)
params.rhoa = 1.206;
% Air drag coefficient (-)
params.ca = 0.29;
% Rolling resistance coefficient (-)
params.cr = 0.01;
% Maximum traction force (N)
params.FtMax = 5e3;
% Minimum traction force (N)
params.FtMin = 0;
% param.FtMin = -1.11e3;
% Maximum breaking force (N)
params.FbMax = 10e3;
% Battery's energy capacity (Wh)
% BMW i3 60Ah - 18.2kWh; BMW i3 94Ah - 27.2kWh; BMW i3 120Ah - 37.9kWh
params.Ecap = 37.9e3;
% Maximum permissible charging time (s)
params.TchMax = 3600;
% Charging power (W)
% 7.4 kW on-board charger on IEC Combo AC, optional 50 kW Combo DC
params.PchMax = 50e3;
% Power dissipation factor (-) (adjusted for Munich - Cologne trip in
% order to achieve realistic BMW i3 range of ~260km)
if trip.type == 1
params.pf = 1;
else
params.pf = 0.4;
end
% Minimum vehicle velocity (km/h)
params.vMin = 30;
% Maximum vehicle velocity (km/h)
params.vMax = 150;
% Minimum SoC (-)
params.SoCmin = 0.1;
% Maximum SoC (-)
params.SoCmax = 0.9;
% Variable vehicle parameters
% Motor efficiency (-)
params.eta = setupMotorEfficiency(params.FtMax);
% Charging power (W)
params.Pch = setupChargingPower(params.PchMax);
% Traction force hyperbola (upper limit) (N)
params.FtMaxHyp = setupTractionForceHyperbola(kmh2ms(params.vMax), params.FtMax);
end
class VehicleParameters:
"""Constant and variable vehicle parameters (not to be changed)"""
def __init__(self, trip):
# Constant vehicle parameters
# The data is obtained from "Technical specifications of the BMW i3 (120 Ah)" valid from 11/2018 and available at https://www.press.bmwgroup.com/global/article/detail/T0285608EN/
# ---------------------------
# Gravitational acceleration (m/s^2)
self.g = 9.81
# Vehicle mass (kg)
self.mv = 1345
# Mass factor (-)
self.eI = 1.06
# Equivalent mass (kg)
self.meq = (1 + self.eI) * self.mv
# Projected frontal area (m^2)
self.Af = 2.38
# Air density (kg/m^3)
self.rhoa = 1.206
# Air drag coefficient (-)
self.ca = 0.29
# Rolling resistance coefficient (-)
self.cr = 0.01
# Maximum traction force (N)
self.FtMax = 5e3
# Minimum traction force (N)
self.FtMin = 0
# self.FtMin = -1.11e3
# Maximum breaking force (N)
self.FbMax = 10e3
# Battery's energy capacity (Wh)
# BMW i3 60Ah - 18.2kWh BMW i3 94Ah - 27.2kWh BMW i3 120Ah - 37.9kWh
self.Ecap = 37.9e3
# Maximum permissible charging time (s)
self.TchMax = 3600
# Charging power (W)
# 7.4 kW on-board charger on IEC Combo AC, optional 50 kW Combo DC
self.PchMax = 50e3
# Power dissipation factor (-) (adjusted for Munich - Cologne trip in order to achieve realistic BMW i3 range of ~260km)
if trip.type == 1:
self.pf = 1
else:
self.pf = 0.4
# Minimum vehicle velocity (km/h)
self.vMin = 30
# Maximum vehicle velocity (km/h)
self.vMax = 150
# Minimum SoC (-)
self.SoCmin = 0.1
# Maximum SoC (-)
self.SoCmax = 0.9
# Variable vehicle parameters
# ---------------------------
# Motor efficiency (-)
self.eta = self.setupMotorEfficiency()
# Charging power (W)
self.Pch = self.setupChargingPower()
# Traction force hyperbola (upper limit) (N)
self.FtMaxHyp = self.setupTractionForceHyperbola()
Trip parameters are defined by the user. Here we focus on two benchmark studies: 1) a \(50\,\mathrm{km}\) long trip with five EV charging stations and low initial SoC; and 2) an actual \(573\,\mathrm{km}\) long Munich - Cologne trip with four EV charging stations and fully charged vehicle.
%% Trip parameters (provided by the user)
% Note: Accuracy and feasibility of the solution are not guaranteed when
% the `trip.reduceSpeed` flag is disabled due to inherent mixed-integer
% nature of the problem!
% Trip type (0 - long (Munich - Cologne); 1 - short)
trip.type = 1;
switch trip.type
case 1
% Spatial discretization step (km)
trip.Ls = 1;
% Trip distance (km)
trip.dist = 50;
% EV charging station locations (km)
trip.kmPosCh = [8, 18, 30, 40, 45];
% Force vehicle to reduce speed at charging locations (1 - yes; 0 - no)
trip.reduceSpeed = 0;
% Initial vehicle speed (km/h)
trip.initSpeed = 30;
% Initial SoC [0, 1]
trip.initSoC = 0.25;
case 0
% Spatial discretization step (km)
trip.Ls = 1;
% Trip distance (km)
trip.dist = 573;
% EV charging station locations (km)
trip.kmPosCh = [110, 150, 250, 375];
% Force vehicle to reduce speed at charging locations (1 - yes; 0 - no)
trip.reduceSpeed = 1;
% Initial vehicle speed (km/h)
trip.initSpeed = 30;
% Initial SoC [0, 1]
trip.initSoC = 0.75;
end
class TripParameters:
"""Trip parameters (to be defined by the user)"""
def __init__(self):
# Note: Accuracy and feasibility of the solution are not guaranteed when the `trip.reduceSpeed` flag is disabled due to inherent mixed-integer nature of the problem!
# Trip type (0 - long (Munich - Cologne) 1 - short)
self.type = 1
assert self.type in [0, 1], 'Incorrect input: trip type should be 0 or 1.'
if self.type == 1:
# Spatial discretization step (km)
self.Ls = 1
# Trip distance (km)
self.dist = 50
# EV charging station locations (km)
self.kmPosCh = np.array([8, 18, 30, 40, 45])
# Force vehicle to reduce speed at charging locations
self.reduceSpeed = False
# Initial vehicle speed (km/h)
self.initSpeed = 30
# Initial SoC [0, 1]
self.initSoC = 0.35
else:
# Spatial discretization step (km)
self.Ls = 1
# Trip distance (km)
self.dist = 573
# EV charging station locations (km)
self.kmPosCh = np.array([110, 150, 250, 375])
# Force vehicle to reduce speed at charging locations
self.reduceSpeed = True
# Initial vehicle speed (km/h)
self.initSpeed = 30
# Initial SoC [0, 1]
self.initSoC = 0.9
You can download the code of this example to try it out for yourself by
clicking here (MATLAB)
or here (Python).
11.19.2. Defining the MPC Problem¶
11.19.2.1. Objective function¶
The primary goal is to minimize the total driving time, i.e. minimize terminal variable \(t_N\) at the last stage \(i=N\):
In addition, we want to minimize the stage cost associated with slack variable \(s, \forall i\in\mathcal{I}\):
where \(\omega_\mathrm{s}\) is an appropriately high weight factor.
Optionally, one could opt for ensuring comfortable driving operation and pursuing energy economy improvements. In such case, additional terms could be included in the stage cost function, e.g.
The second term imposes a penalty on consumed energy during driving by reducing the applied traction force, whereas the third term minimizes the total braking force. The corresponding weight factors \(\omega_\mathrm{e}\) and \(\omega_\mathrm{b}\) provide a trade-off between different objectives. Furthermore, one could also penalize jerking, i.e. a change in the traction force between consecutive steps, using another slack variable.
The cost functions are coded in MATLAB and Python as follows:
% Assume variable ordering zi = [u{i}; x{i}] for i=1...N
% zi = [slack(i); Ft(i); Fb(i); deltaTch(i); v(i); t(i); SoC(i)]
% pi = [vMax(i); vMin(i); alpha(i); TchMax(i); Ls(k)] #k - iteration No.
% Objective function
R = [ 1e-7, 0;
0, 1e-6];
slackCostFactor = 1e6;
model.objective = @(z) slackCostFactor*z(1) + [z(2); z(3)]'*R*[z(2); z(3)];
model.objectiveN = @(z) z(6);
""""
Assume variable ordering zi = [u{i}, x{i}] for i=1...N
zi = [slack{i}, Ft{i}, Fb{i}, deltaTch{i}, v{i}, t{i}, SoC{i}]
pi = [vMax{i}, vMin{i}, alpha{i}, TchMax{i}, Ls{k}] #k - iteration No.
""""
# Objective function
R = np.diag([1e-7, 1e-6])
slackCostFactor = 1e6
model.objectiveN = (lambda z: z[5])
model.objective = (lambda z: slackCostFactor * z[0])
# model.objective = (lambda z: slackCostFactor * z[0] + casadi.horzcat(z[1], z[2]) @ R @ casadi.vertcat(z[1], z[2]))
11.19.2.2. Equality constraints¶
The equality constraints model.eq in this example results from the vehicle’s dynamics and energetics model given above, and is implemented as follows:
% Problem dimensions
nx = 3;
nu = 4;
np = 5;
nh = 6;
model.N = round(trip.dist/trip.Ls); % horizon length
if mod(model.N,1)~=0
error('Incorrect input: trip distance should be an exact multiple of the spatial discretization step.');
end
model.nvar = nx + nu; % number of variables
model.neq = nx; % number of equality constraints
model.nh = nh; % number of inequality constraints
model.npar = np; % number of runtime parameters
% Dynamics, i.e. equality constraints
model.eq = @(z,p) [sqrt(ForcesMax(2*p(5)/param.meq*(z(2) - z(3) - param.cr*param.mv*param.g*cos(p(3)) - param.mv*param.g*sin(p(3)) - 0.5*param.ca*param.Af*param.rhoa*z(5)^2) + z(5)^2, 0));
z(6) + p(5)/z(5) + z(4);
z(7) - param.pf*p(5)*z(2)/(3600*param.eta(z(2))*param.Ecap) + param.Pch(z(7))*z(4)/(3600*param.Ecap)];
model.E = [zeros(nx,nu),eye(nx)];
% Initial and final conditions
model.xinitidx = nu+1:nu+nx;
# Problem dimensions
nx = 3
nu = 4
npar = 5
nh = 6
model = forcespro.nlp.SymbolicModel()
model.N = round(trip.dist / trip.Ls); # horizon length
assert model.N % 1 == 0, 'Incorrect input: trip distance should be an exact multiple of the spatial discretization step'
model.nvar = nx + nu; # number of variables
model.neq = nx; # number of equality constraints
model.nh = nh; # number of inequality constraints
model.npar = npar; # number of runtime parameters
# Objective function
R = np.diag([1e-7, 1e-6])
slackCostFactor = 1e6
# model.objective = (lambda z: casadi.horzcat(z[1], z[2]) @ R @ casadi.vertcat(z[1], z[2]))
model.objective = (lambda z: slackCostFactor * z[0])
model.objectiveN = (lambda z: z[5])
# Dynamics, i.e. equality constraints
model.eq = lambda z, p: casadi.vertcat( np.sqrt(forcespro.modelling.smooth_max(2 * p[4] /
param.meq * (z[1] - z[2] - param.cr * param.mv * param.g * np.cos(p[2]) - param.mv * param.g * np.sin(p[2]) - 0.5 * param.ca * param.Af * param.rhoa * z[4]**2) + z[4]**2, 0)),
z[5] + p[4] / z[4] + z[3],
z[6] - param.pf * p[4] * z[1] / (3600 * param.eta(z[1])* param.Ecap) + param.Pch(z[6]) * z[3] / (3600 * param.Ecap))
model.E = np.concatenate([np.zeros((nx, nu)), np.eye(nx)], axis=1)
# Initial and final conditions
model.xinitidx = np.arange(nu, nu + nx);
The use of smooth maximum approximation (see section Section 20.3) ensures a nonnegative square root term and thus a feasible solution.
11.19.2.3. Inequality constraints¶
The inequality constraints model.ineq comprise all decision variable bounds described previously. For purposes of model feasibility, two additional trivial constraints pertaining to the vehicle velocity’s square root term are included in the model, as shown in the code-snippets.
%% Inequality constraints
% Upper/lower variable bounds lb <= z <= ub
% inputs | states
% slack Ft Fb Tch v t SoC
model.lb = [0, param.FtMin, 0., 0., kmh2ms(param.vMin), 0., 0.];
model.ub = [0.1, param.FtMax, param.FbMax, param.TchMax, kmh2ms(param.vMax), +inf, 1.];
% Nonlinear inequalities hl <= h(z,p) <= hu
model.ineq = @(z,p) [z(2) - param.FtMaxHyp(z(5));
z(4) - p(4);
z(7) - param.SoCmax - z(1);
param.SoCmin - z(7) - z(1);
2*p(5)/param.meq*(z(2) - z(3) - param.cr*param.mv*param.g*cos(p(3)) - param.mv*param.g*sin(p(3)) - 0.5*param.ca*param.Af*param.rhoa*z(5)^2) + z(5)^2 - kmh2ms(ForcesMax((1-z(4))*p(1), param.vMin+1))^2;
kmh2ms(p(2))^2 - (2*p(5)/param.meq*(z(2) - z(3) - param.cr*param.mv*param.g*cos(p(3)) - param.mv*param.g*sin(p(3)) - 0.5*param.ca*param.Af*param.rhoa*z(5)^2) + z(5)^2)];
% Upper/lower bounds for inequalities
model.hu = [0, 0, 0, 0, 0, 0];
model.hl = [-inf, -inf, -inf, -inf, -inf, -inf];
# Inequality constraints
# Upper/lower variable bounds lb <= z <= ub
# inputs | states
# slack Ft Fb Tch v t SoC
model.lb = np.array([0., param.FtMin, 0., 0., kmh2ms(param.vMin), 0., 0.])
model.ub = np.array([0.1, param.FtMax, param.FbMax, param.TchMax, kmh2ms(param.vMax), np.inf, 1.])
# Nonlinear inequalities hl <= h(z,p) <= hu
model.ineq = lambda z,p: casadi.vertcat(z[1] - param.FtMaxHyp(z[4]),
z[3] - p[3],
z[6] - param.SoCmax - z[0],
param.SoCmin - z[6] - z[0],
2 * p[4] / param.meq * (z[1] - z[2] - param.cr * param.mv * param.g * np.cos(p[2]) - param.mv * param.g * np.sin(p[2]) - 0.5 * param.ca * param.Af * param.rhoa * z[4]**2) + z[4]**2 - kmh2ms(forcespro.modelling.smooth_max((1 - z[3]) * p[0], param.vMin + 1))**2,
kmh2ms(p[1])**2 - (2 * p[4] / param.meq * (z[1] - z[2] - param.cr * param.mv * param.g * np.cos(p[2]) - param.mv * param.g * np.sin(p[2]) - 0.5 * param.ca * param.Af * param.rhoa * z[4]**2) + z[4]**2))
# Upper/lower bounds for inequalities
model.hu = np.array([0, 0, 0, 0, 0, 0])
model.hl = np.array([-np.inf, -np.inf, -np.inf, -np.inf, -np.inf, -np.inf])
11.19.2.4. Generating the FORCESPRO NLP solver¶
To generate a suitable NLP solver for our MPC problem one needs to provide the model and codeoptions. The model has been populated above and we now specify the desired codeoptions and generate the solver by calling FORCES_NLP. The following code-snippets show how this can be done:
%% Generate FORCESPRO solver
% Define solver options
codeoptions = getOptions('FORCESNLPsolver');
codeoptions.printlevel = 0;
codeoptions.nlp.compact_code = 1;
% Generate code
FORCES_NLP(model, codeoptions);
# Generate FORCESPRO solver
# -------------------------
# Define solver options
codeoptions = forcespro.CodeOptions("FORCESNLPsolver")
codeoptions.printlevel = 0
codeoptions.nlp.compact_code = 1
# Generate code
solver = model.generate_solver(codeoptions)
11.19.2.5. Calling the solver¶
Once the solver has been generated it needs to be provided with initial and runtime parameters. In this example we are running a single full-horizon snapshot instead of a traditional rolling-horizon MPC, as follows:
function [ sim ] = runSimulation(trip, param, model)
% Defines initial and stage-dependent runtime parameters and solves the
% problem
%% Define spatially distributed (i.e. stage-dependent) parameters
% Road speed limits and slope angles
[vMaxRoad, ~, vMinRoad, roadSlope] = setupRoadParameters(param.vMin, trip);
% Maximum permissible charging time
deltaTchMax = setupChargingTime(param.TchMax, trip);
%% Initialize the problem
problem.x0 = zeros(model.N*model.nvar,1);
sim.kMax = trip.dist/trip.Ls;
np = model.npar;
if trip.initSpeed < param.vMin || trip.initSpeed > param.vMax
v1 = kmh2ms(param.vMin);
warning('Initial vehicle speed is outside of the speed limits. It will be set to the minimum speed limit at t=0.')
else
v1 = kmh2ms(trip.initSpeed);
end
if trip.initSoC < param.SoCmin || trip.initSoC > param.SoCmax
SoC1 = 0.5;
warning('Initial vehicle state-of-charge is outside of the limits. It will be set to 50% at t=0.')
else
SoC1 = trip.initSoC;
end
% X(1) = [v(1); t(1); SoC(1)]
problem.xinit = [v1; 0; SoC1];
%% Solve the problem
% Set runtime parameters
problem.all_parameters = zeros(np*model.N,1);
for i = 1:model.N
problem.all_parameters((i-1)*np+1:i*np) = [vMaxRoad(i); vMinRoad(i); roadSlope(i*trip.Ls*1e3); deltaTchMax(i); trip.Ls*1e3];
end
% Call solver
[solverout,exitflag,info] = FORCESNLPsolver(problem);
sim.exitflag = exitflag;
% Extract state and control vector
if exitflag == 1
sim.Z = unpackStruct(solverout,model.nvar);
sim.solvetime = info.solvetime;
sim.iters = info.it;
else
error('Some problem in solver.');
end
end
def runSimulation(trip, param, model, solver):
"""Defines initial and stage-dependent runtime parameters and solves the problem"""
x0 = np.zeros(model.N * model.nvar)
problem = {"x0": x0}
kMax = model.N
npar = model.npar
# Initialize system states
# ------------------------
assert trip.initSpeed >= param.vMin or trip.initSpeed <= param.vMax, 'Initial vehicle speed is outside of the speed limits.'
assert trip.initSoC >= param.SoCmin or trip.initSoC <= param.SoCmax, 'Initial vehicle state-of-charge is outside of the limits.'
# Initialize the problem
# X(1) = [v(1); t(1); SoC(1)]
problem["xinit"] = [kmh2ms(trip.initSpeed), 0, trip.initSoC]
# Define spatially distributed (i.e. stage-dependent) parameters
# --------------------------------------------------------------
# Road speed limits and slope angles
vMaxRoad, _, vMinRoad, roadSlope = setupRoadParameters(param.vMin, trip)
# Maximum permissible charging time
deltaTchMax = setupChargingTime(param.TchMax, trip);
# Set runtime parameters
problem["all_parameters"] = np.zeros(npar * model.N)
for i in range(model.N):
problem["all_parameters"][i * npar : (i + 1) * npar] = np.array([vMaxRoad[i], vMinRoad[i], roadSlope((i + 1) * trip.Ls * 1e3).item(), deltaTchMax[i], trip.Ls * 1e3])
# Solve the problem
# -----------------
solverout, exitflag, info = solver.solve(problem)
assert exitflag == 1, 'Some problem in solver.'
sim = {"exitflag": exitflag}
sim["Z"] = unpackDict(solverout)
sim["kMax"] = kMax
sim["solvetime"] = info.solvetime
sim["iters"] = info.it
sim = displayResults(sim);
return sim
11.19.2.6. Results¶
We consider two trips of different lengths previously described in section Section 11.19.1.5 with three benchmark studies conducted for the shorter trip and two studies for the longer trip:
a short trip of \(50\,\mathrm{km}\) with arbitrarily generated road profile, \(5\) charging stations along the road, and vehicle’s initial SoC of: a) \(75\,\%\); b) \(50\,\%\); and c) \(25\,\%\).
a long trip of \(573\,\mathrm{km}\) representing a Munich - Cologne trip with actual road profile, vehicle’s initial SoC of \(90\,\%\), and: a) \(4\) charging stations along the road; and b) \(2\) charging stations along the road.
Studies 1a - 1c have the same allocation of charging stations, with chargers placed at \(8\,\mathrm{km}\), \(18\,\mathrm{km}\), \(30\,\mathrm{km}\), \(40\,\mathrm{km}\) and \(45\,\mathrm{km}\) marks. Furthermore, we allow optional charging for all three studies. On the other hand, a Munich - Cologne trip 2a considers four chargers placed at \(110\,\mathrm{km}\), \(150\,\mathrm{km}\), \(250\,\mathrm{km}\) and \(375\,\mathrm{km}\), while trip 2b has two available chargers at \(150\,\mathrm{km}\) and \(375\,\mathrm{km}\). In contrast to the short trip, here we impose mandatory charging requirement. The most notable trip metrics for all five studies are showcased in Table 11.1.
Trip |
Distance |
SoC (t=0) |
# stations |
# stops |
Total time |
Charge time |
|---|---|---|---|---|---|---|
1a |
50 km |
75 % |
5 |
0 |
34.14 min |
0 min |
1b |
50 km |
50 % |
5 |
0 |
44.56 min |
0 min |
1c |
50 km |
25 % |
5 |
1 |
51.82 min |
16.3 min |
2a |
573 km |
90 % |
4 |
4 |
345.03 min |
66.52 min |
2b |
573 km |
90 % |
2 |
2 |
346.91 min |
68.81 min |
The simulation results for studies 1a and 1b are depicted in Figure 11.68 and Figure 11.69, respectively. Since the vehicle has sufficiently high SoC, the charging is not needed in both cases. However, in the second trip the vehicle is forced to reduce its velocity significantly below the speed limit in order to preserve energy and complete the trip with sufficient battery charge, which leads to a higher trip time.
A low initial SoC in study 1c forces the vehicle to charge, as shown in Figure 11.70, which leads to an even higher trip time. The EV decides to stop at the first charging stop and charge just enough to complete the trip with the SoC at the lower bound.
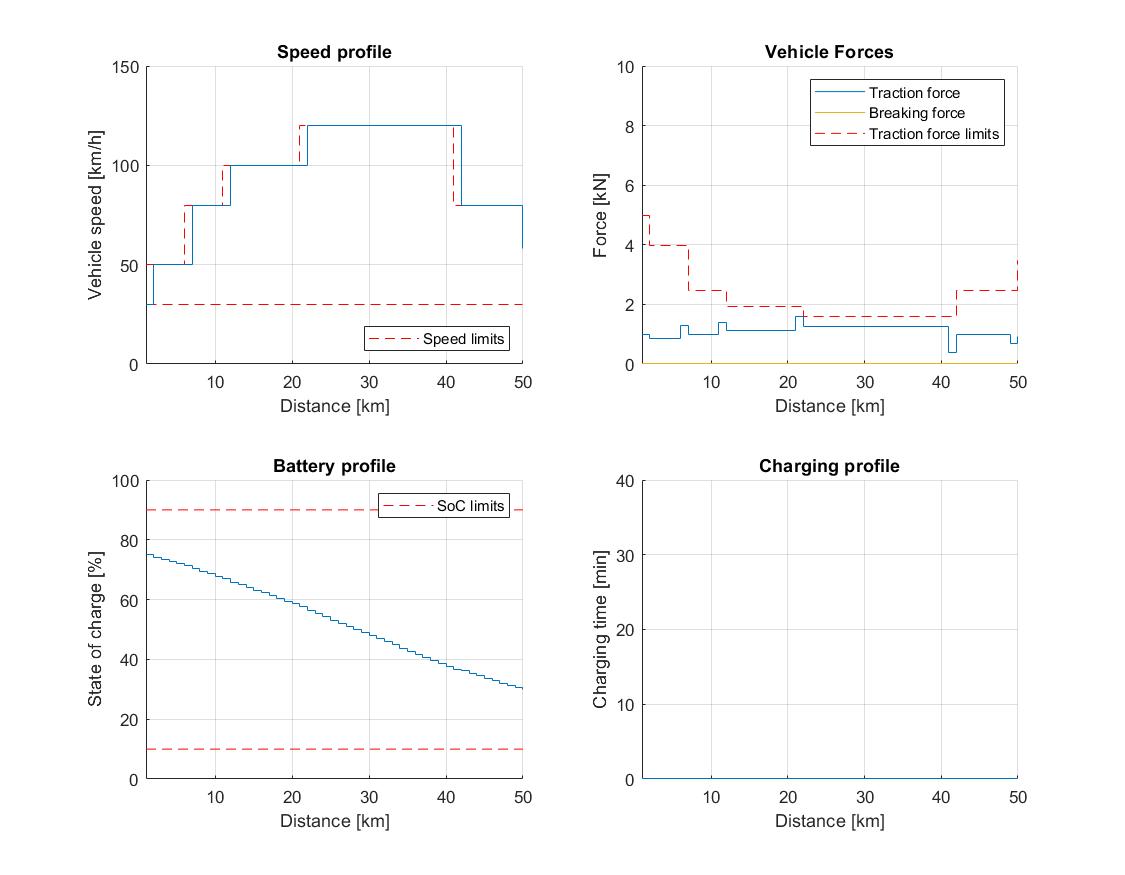
Figure 11.68 Vehicle performance on a short trip with 5 charging stations and 75 % initial SoC.¶
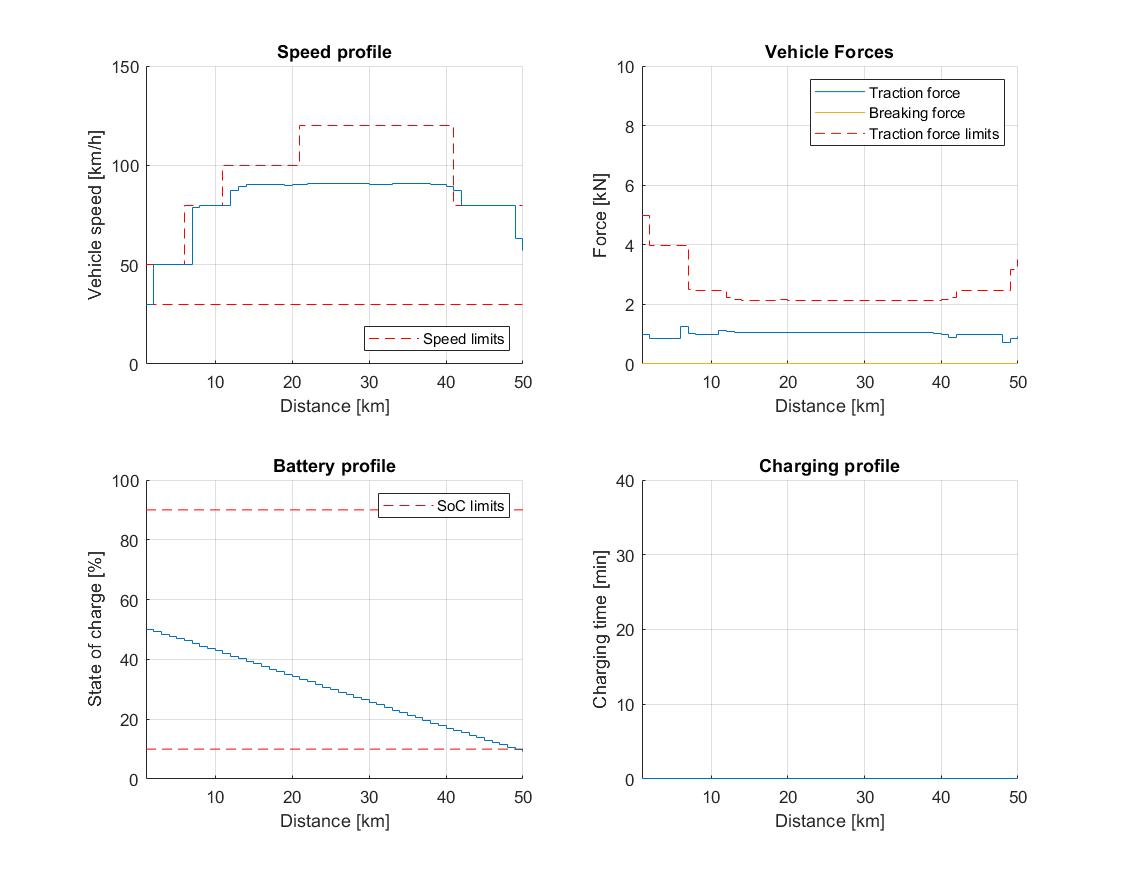
Figure 11.69 Vehicle performance on a short trip with 5 charging stations and 50 % initial SoC.¶
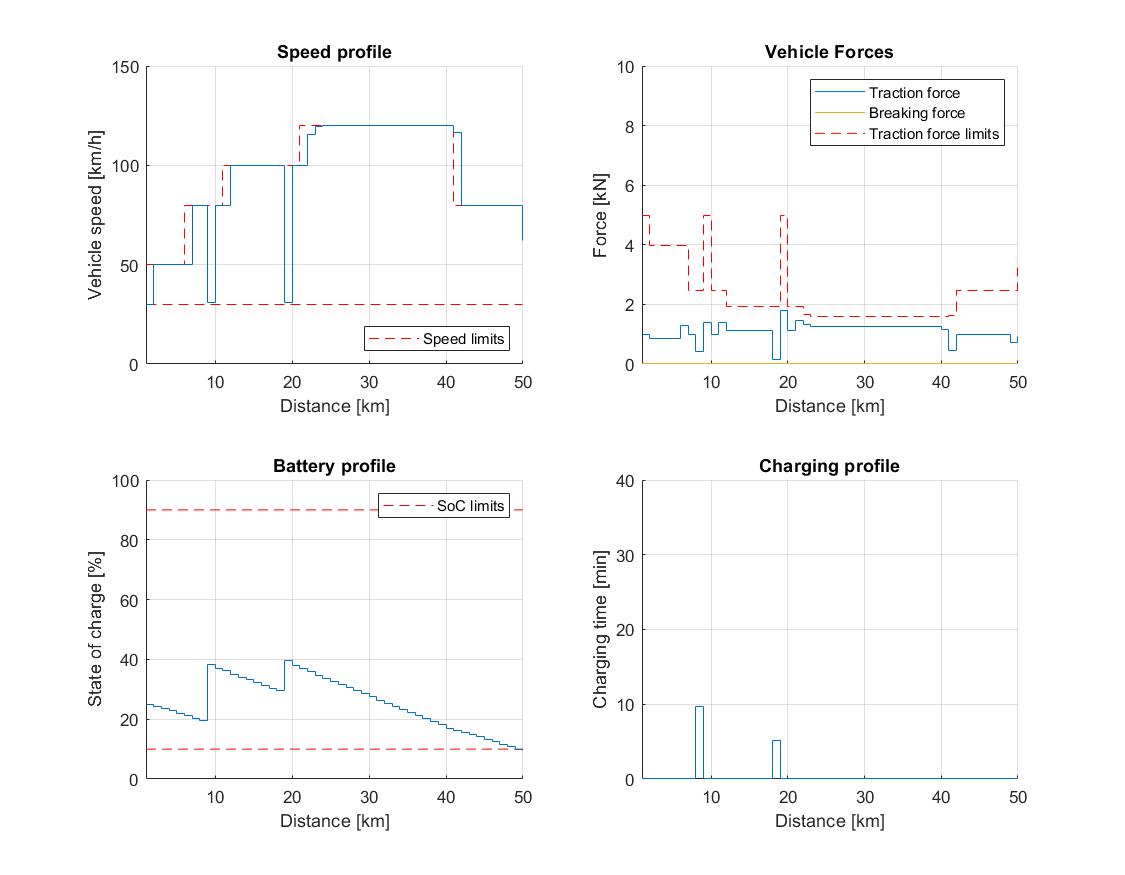
Figure 11.70 Vehicle performance on a short trip with 5 charging stations and 25 % initial SoC.¶
The longer trip studies with mandatory charging presented in Figure 11.71 and Figure 11.72 again indicate that the EV will complete the trip at the minimum permissible SoC in order to minimize the total charging time. The results also suggest that the vehicle will intentionally reduce speed in order to preserve energy: the availability of only 2 chargers in study 2b forces the vehicle to slightly reduce speed midway through the trip. The overall trip time increases by \(0.55\,\%\), and the total charging time is \(3.44\,\%\) bigger compared to study 2a.
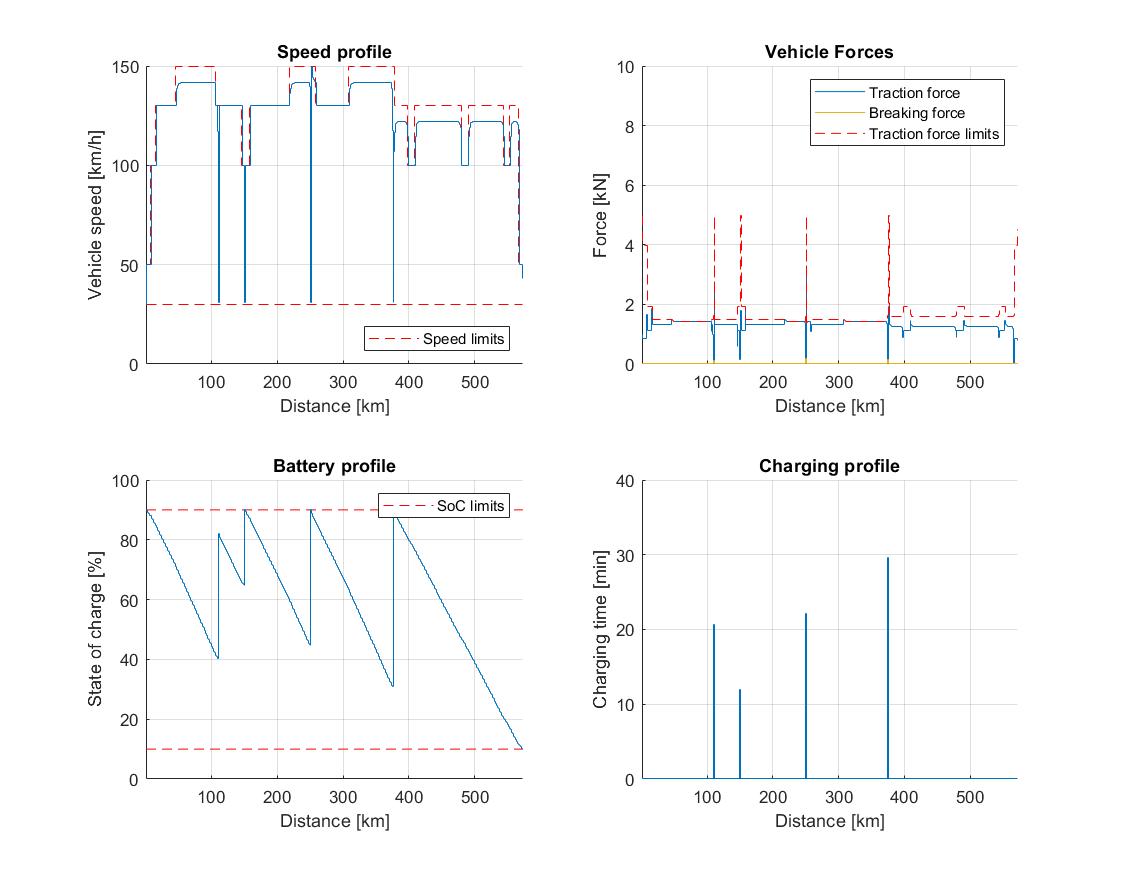
Figure 11.71 Vehicle performance on a long trip with 4 charging stations and 90 % initial SoC.¶

Figure 11.72 Vehicle performance on a long trip with 2 charging stations and 90 % initial SoC.¶
Jia Y.; Jibrin, R.; Itoh Y.; Görges, D.: Energy-Optimal Adaptive Cruise Control for Electric Vehicles in Both Time and Space Domain based on Model Predictive Control. In: IFAC-PapersOnLine, vol. 50, no. 2, 2017, pp. 13-20, 2019.
Jia, Y.; Jibrin, R.; Görges, D.: Energy-Optimal Adaptive Cruise Control for Electric Vehicles Based on Linear and Nonlinear Model Predictive Control. In: IEEE Transactions on Vehicular Technology, vol. 69, no. 12, pp. 14173-14187, Dec. 2020.
Fastned: Charging with a BMW i3, https://support.fastned.nl/hc/en-gb/articles/204784718-Charging-with-a-BMW-i3
X-engineer: Why do we need gears?, https://x-engineer.org/need-gears/
BMW Group: Technical specifications of the BMW i3 (120 Ah), https://www.press.bmwgroup.com/global/article/detail/T0285608EN/