11.10. High-level interface: Indoor localization (MATLAB & Python)

The indoor localization problem is to estimate the position of a target by measurements from various anchors with known location. Outdoors, this well known as GPS, while indoors other frequency bands (and less accurate clocks) are usually used. In this example, we show how to generate code for a position estimator that relies on time-of-flight (TOF) measurements (GPS uses time-difference-of-arrival, TDOA). The latter can be easily implemented with FORCESPRO as well with only minor changes to the code below.

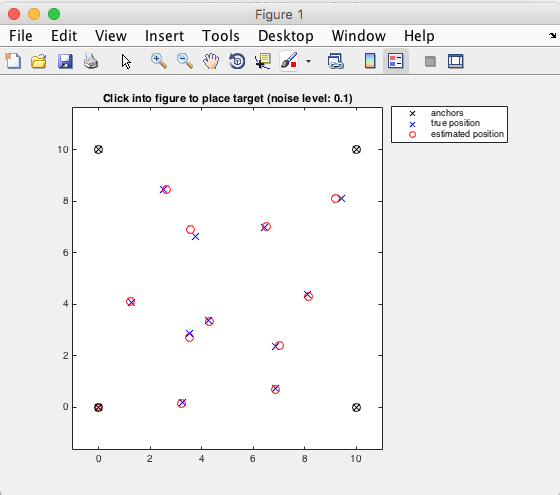
Figure 11.35 Indoor localization example GUI.

You can download the MATLAB code of this example to try it out for yourself by clicking here (MATLAB) or here (Python).

Running the code will produce an interactive window like in Figure 11.35.

11.10.1. Time of flight measurements

Given \(N\) anchors with known positions \((x_i^a,y_i^a)\), \(i=1,\dots,N\), the distance to the target with unknown position \((x,y)\) is given by:

\[d_i = ct_i = \sqrt{(x-x_i^a)^2 + (y-y_i^a)^2}\]

where \(t_i\) is the time the signal from anchor \(i\) travels at the speed \(c=299\,792\,458\,\mathrm{m/s}\)

11.10.2. Estimation error

Instead of the real distance, we work with squared distances to define the estimation error:

\[e_i = (x-x_i^a)^2 + (y-y_i^a)^2 - d_i^2\]

11.10.3. Minimize the error

The objective is a least-squares error function:

\[\min_{x,y} \sum_{i=1}^N e_i^2\]

11.10.4. Implementation

The following MATLAB/Python code generates C-code for implementing an optimizer for minimizing the least-squares error function from above. It takes the anchor positions and the distance measurements, and returns the estimated position of the target.

MatlabPython

%% This function generates the estimator
function [] = generateEstimator(numberOfAnchors,xlimits,ylimits)
% Generates 2D decoding code for localization using FORCESPRO NLP

    na = numberOfAnchors;

    %% NLP problem definition
    % no need to change anything below
    model.N = 1;      % number of distance measurements
    model.nvar = 2;   % number of variables (use 3 if 3D)
    model.npar = numberOfAnchors*3; % number of parameters: coordinates of anchors in 2D, plus measurements
    model.objective = @(z,p) objective(z,p,na);
    model.lb = [xlimits(1) ylimits(1)]; % lower bounds on (x,y)
    model.ub = [xlimits(2) ylimits(2)]; % upper bounds on (x,y)

    %% codesettings
    codesettings = getOptions('localizationDecoder');
    codesettings.printlevel = 0; % set to 2 to see some prints
    % codesettings.server = 'http://winner10:2470';
    codesettings.maxit = 50; % maximum number of iterations
    codesettings.nlp.ad_tool = 'casadi';
    %codesettings.nlp.ad_tool = 'symbolic-math-tbx';

    %% generate code
    FORCES_NLP(model, codesettings);

end

%% This function implements the objective
% We assume that the parameter vector p is ordered as follows:
% p(1:na)        - x-coordinates of the anchors
% p(na+(1:na))   - y-coordinates of the anchors
% p(2*na+(1:na)) - distance measurements of the anchors
function [ obj ] = objective(z, p, na)

    obj=0;
    for i = 1:na
        obj = obj + ( (p(i)-z(1))^2 + (p(i+na)-z(2))^2 - p(i+2*na)^2 )^2;
    end
end